SUBHEAD: Historic 'tile' discovery gives math world a big jolt. First of its kind in 30 years.
By David Freeman on 19 August 2015 for Huffington Post -
(http://www.huffingtonpost.com/entry/historic-tile-discovery-gives-math-world-a-big-jolt_55d3e39ce4b07addcb4495ba)

Image above: A plane tiled with the newly identified pentagon. From original article.
A team of mathematicians has wowed the math world with their discovery of a new kind of pentagon capable of "tiling a plane"--that is, fitting together on a flat surface without overlapping or leaving any gaps.
It's said to be only the fifteenth such pentagon ever found and the first new one to be found in 30 years. Finding one is a bit like discovering a new atomic particle, Dr. Casey Mann, associate professor of mathematics at the University of Washington in Bothell and a member of the team, said in a written statement.
The team made the find with the help of a computer program designed just for the purpose.
"We discovered the tile using a computer to exhaustively search through a large but finite set of possibilities," Mann told The Guardian, adding that the team had been "a bit surprised" to find the new type of pentagon.
In addition to Mann, the team includes Dr. Jennifer McLoud-Mann, who is also an associate professor of math at the university, and David Von Derau, a recent graduate of the university.
Along with suggesting a new way to tile a bathroom floor, Mann said the discovery could lead to advances in chemistry and structural design--specifically in the study of crystals and in the emerging field of self-assembly, in which scientists aim to create structures that come together all on their own as a result of their shapes and other properties.
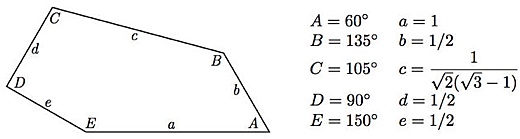
Image above: Details of the newly identified pentagon. From original article.
Of course, tiling patterns (also known as tessellations) hold significant aesthetic appeal--at least for mathematicians.
"Mainly we study them for pure pleasure," Dr. Steven Strogatz, a Cornell University mathematician who was not involved in the discovery, told The Huffington Post in an email. He called the new discovery "cool" and pointed out that tessellations also show up in quilts, wallpaper designs, and honeycombs as well as buildings like the Alhambra and Escher woodcuts like this one.
The discovery adds to a curious set of facts about tessellations and convex polygons (conventional ones with outward-pointing corners).
Mathematicians have proven that no convex polygons with more than six sides can tile a plane, according to Mann. All triangles and quadrilaterals can, as can three kinds of hexagon.
It's clear that regular pentagons (those with equal sides and angles) cannot tile a plane. As for how many kinds of irregular pentagons can, Mann said no one knows for sure--and the discovery of the new one doesn't change that.
"After over 100 years of looking, we still do not know if we have found all types of convex pentagons that tile the plane," he said in the email. "It is a fascinating mathematical riddle!"
.
By David Freeman on 19 August 2015 for Huffington Post -
(http://www.huffingtonpost.com/entry/historic-tile-discovery-gives-math-world-a-big-jolt_55d3e39ce4b07addcb4495ba)

Image above: A plane tiled with the newly identified pentagon. From original article.
A team of mathematicians has wowed the math world with their discovery of a new kind of pentagon capable of "tiling a plane"--that is, fitting together on a flat surface without overlapping or leaving any gaps.
It's said to be only the fifteenth such pentagon ever found and the first new one to be found in 30 years. Finding one is a bit like discovering a new atomic particle, Dr. Casey Mann, associate professor of mathematics at the University of Washington in Bothell and a member of the team, said in a written statement.
The team made the find with the help of a computer program designed just for the purpose.
"We discovered the tile using a computer to exhaustively search through a large but finite set of possibilities," Mann told The Guardian, adding that the team had been "a bit surprised" to find the new type of pentagon.
In addition to Mann, the team includes Dr. Jennifer McLoud-Mann, who is also an associate professor of math at the university, and David Von Derau, a recent graduate of the university.
Along with suggesting a new way to tile a bathroom floor, Mann said the discovery could lead to advances in chemistry and structural design--specifically in the study of crystals and in the emerging field of self-assembly, in which scientists aim to create structures that come together all on their own as a result of their shapes and other properties.

Image above: Details of the newly identified pentagon. From original article.
Of course, tiling patterns (also known as tessellations) hold significant aesthetic appeal--at least for mathematicians.
"Mainly we study them for pure pleasure," Dr. Steven Strogatz, a Cornell University mathematician who was not involved in the discovery, told The Huffington Post in an email. He called the new discovery "cool" and pointed out that tessellations also show up in quilts, wallpaper designs, and honeycombs as well as buildings like the Alhambra and Escher woodcuts like this one.
The discovery adds to a curious set of facts about tessellations and convex polygons (conventional ones with outward-pointing corners).
Mathematicians have proven that no convex polygons with more than six sides can tile a plane, according to Mann. All triangles and quadrilaterals can, as can three kinds of hexagon.
It's clear that regular pentagons (those with equal sides and angles) cannot tile a plane. As for how many kinds of irregular pentagons can, Mann said no one knows for sure--and the discovery of the new one doesn't change that.
"After over 100 years of looking, we still do not know if we have found all types of convex pentagons that tile the plane," he said in the email. "It is a fascinating mathematical riddle!"
.
No comments :
Post a Comment